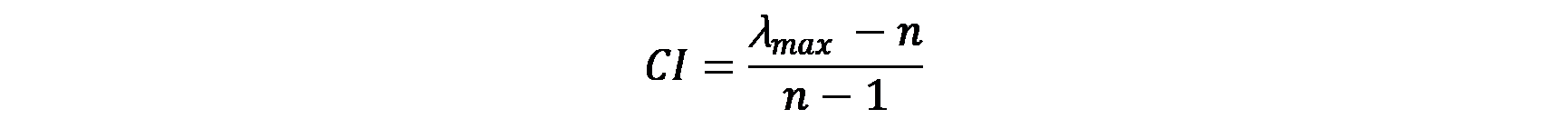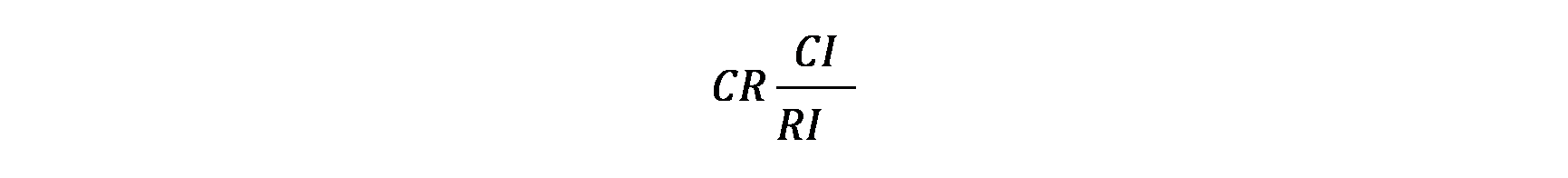建模学习(一)
十大模型和其涉及算法
| 十大模型 | 对应的最常用的算法 |
|---|---|
| 评价类模型 | 层次分析法、TOPSIS法(优劣解距离法) |
| 插值与拟合模型 | 多项式值、分段插值、Hermite插值、样条插值(一维)、n维数据的插值、cftool工具箱 |
| 相关性模型 | 相关系数、皮尔逊person和斯皮尔曼spearman、典型型相关分析 |
| 回归模型 | 多元回归分析、逐步回归分析、岭回归和Lasso回归 |
| 图论模型 | Dijkstra迪杰斯特拉算法、Floyd算法 |
| 分类问题 | 二分类:logisyic回归、Fisher判别分析、SVM支持向量机;多分类:多分类Logisic回归模型 |
| 聚类模型 | K-Means++算法、DBSCAN聚类算法 |
| 时间序列模型 | AR、MA、ARMA模型;ARCH模型和GARCH模型;单位根时间序列 |
| 预测模型 | 插值预测、时间序列预测、灰色预测模型、BP神经网络 |
| 降维模型 | SVD奇异值分解(图像处理)、主成分分析、因子分析 |
层次分析法
(The analytic hierarchy process,简称AHP)
主要用于解决评价类问题,例如:方案选择、哪位运动员给或者员工表现更优秀
评价类问题
1、评价类问题可用打分解决
使用打分法解决评价问题,只需要补充下表
| 指标权重 | 方案1 | 方案2 | … | |
|---|---|---|---|---|
| 指标1 | ||||
| 指标2 | ||||
| 指标3 | ||||
| … |
表中各指标的指标权重和为1,各指标方案和也为1,它们表示针对某一因素所占的权重。
2、解决评价类问题,要思考以下问题:
1.我们评价的目标或目的是什么?(如:旅游最佳目的地的选择、最佳员工的选择,其中目的地与最佳员工就是我们评价的目标)
2.我们为了达到这个目标可选的方案有哪些?(如:旅游问题的目的地,员工问题的候选人)
3.评价的准则(指标)是什么?(是根据什么标准或划分哪些因素,做出评价。如:旅游问题的食住行)
前两个问题的答案一般可以分析题目得出,第三个问题需要结合题中的背景材料、常识以及网上搜集到的参考资料(知网等平台搜索)进行分析,从而选出最合适的指标。也可以小组进行讨论、搜索专家看法或调查问卷来获取需要的指标。 推荐网站:虫部落
我们对指标权重的确定,一次性考虑三个或三个以上指标之间的关系时,往往会考虑不周。
所以我们用对指标进行两两比较,根据两两比较的结果来推算权重。
层次分析法可以通过重要程度表给出的规定来进行两个因素之间的比较。
| 标度 | 含义 |
|---|---|
| 1 | 表示两个因素相比,同样重要 |
| 3 | 表示两个因素相比,一个因素比另一个因素稍微重要 |
| 5 | 表示两个因素相比,一个因素比另一个因素明显重要 |
| 7 | 表示两个因素相比,一个因素比另一个因素强烈重要 |
| 9 | 表示两个因素相比,一个因素比另一个因素极端重要 |
| 2,4,6,8 | 上述两相邻判断的中值 |
| 倒数 | A和B相比如果标度为3,那么B和A想必就是1/3 |
层次分析法解题步骤
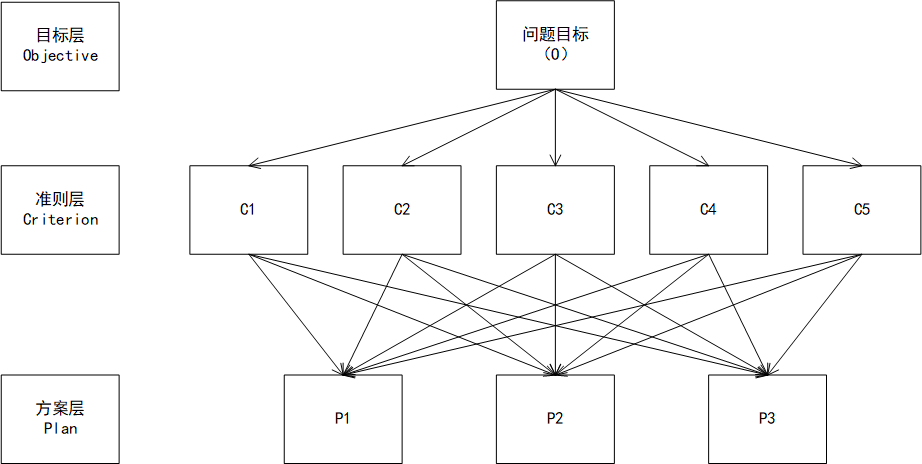
1、分析系统中各因素的关系,建立系统的递阶层次结构
2、构造判断矩阵
| Cn | P1 | P2 | P3 |
|---|---|---|---|
| P1 | |||
| P2 | |||
| P3 |
在构造判断矩阵时,矩阵中的数需要自己填写。在论文表达上可不做体现,直接给出相应判断矩阵即可。
准则层——方案层的判断矩阵要结合实际来填写,如果题目中有其他数据,可以考虑利用这些数据进行计算。3、计算权重
由判断矩阵计算被比较元素对于该准则的相对权重,并进行一致性检验。
计算权重的方法
(1)算术平均法 (2)几何平均法 (3)特征值法
进行比赛时三种方法都使用,这样可以保证结果的稳健性,得出的结论更全面、有效,让人信服。
写作示例
为了保证结果的稳健性(稳定性),本文分别采用算术平均法、几何平均法、特征值法三种方法分别得出权重,再根据得到的权重矩阵计算各方案的得分,并进行排序和综合分析,这样避免了采用单一方法所产生的偏差,所得出的结论(结果)将更全面、更有效。
4、进行一致性检验
一致性检验的步骤
1、计算一致性指标CI
2、查找对应的平均随机一致性指标RI
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RI | 0 | 0 | 0.52 | 0.89 | 1.12 | 1.26 | 1.36 | 1.41 | 1.46 | 1.49 | 1.52 | 1.54 | 1.56 | 1.58 | 1.59 |
注:在实际运用中,n很少超过10,如果指标的个数大于10,则可考虑建立二级指标体系
3、计算一致性比例CR
如果CR > 0.1,则可以认为判断矩阵的一致性可以接受;否则需要对判断矩阵进行修正。
因为一致矩阵性矩各行成倍数关系,需要调整的判断矩阵可通过此性质进行调整
4、计算个层元素对系统目标层的合成权重,并进行排序
合成权重=不同方案对应指标的权重 × 指标权重
层次分析法的一些局限性
1、评价的决策层不能太多,太多n会很大,判断矩阵和一致性矩阵差异可能会很大。(n<=15)
2、如果决策层中指标数据已知,不适合用层次分析。
如果决策层中指标数据已知,我们可以采用TOPSIS法解决此类问题。TOPSIS