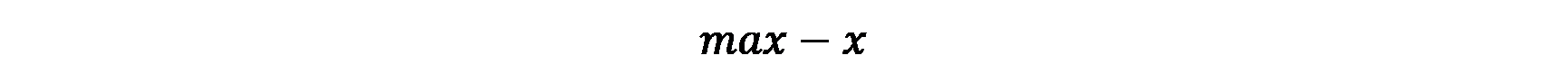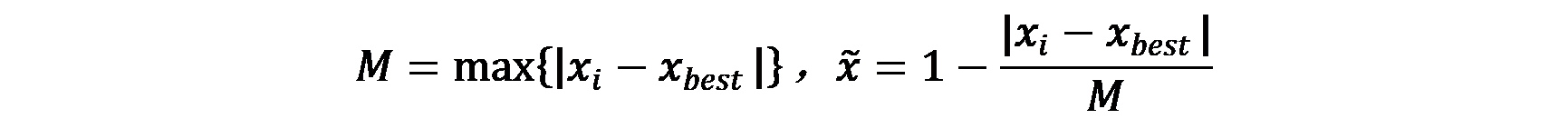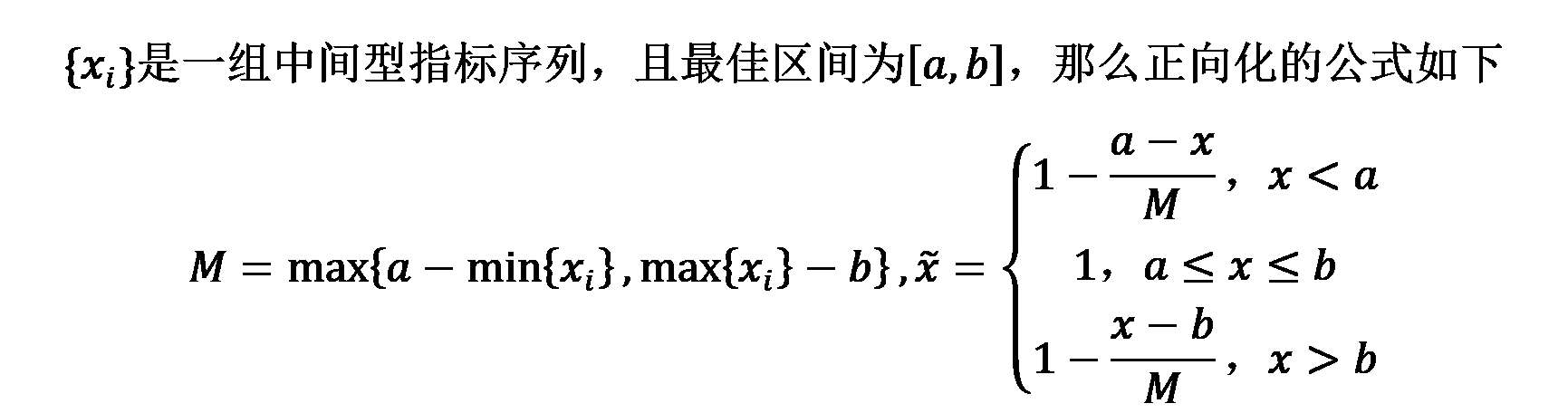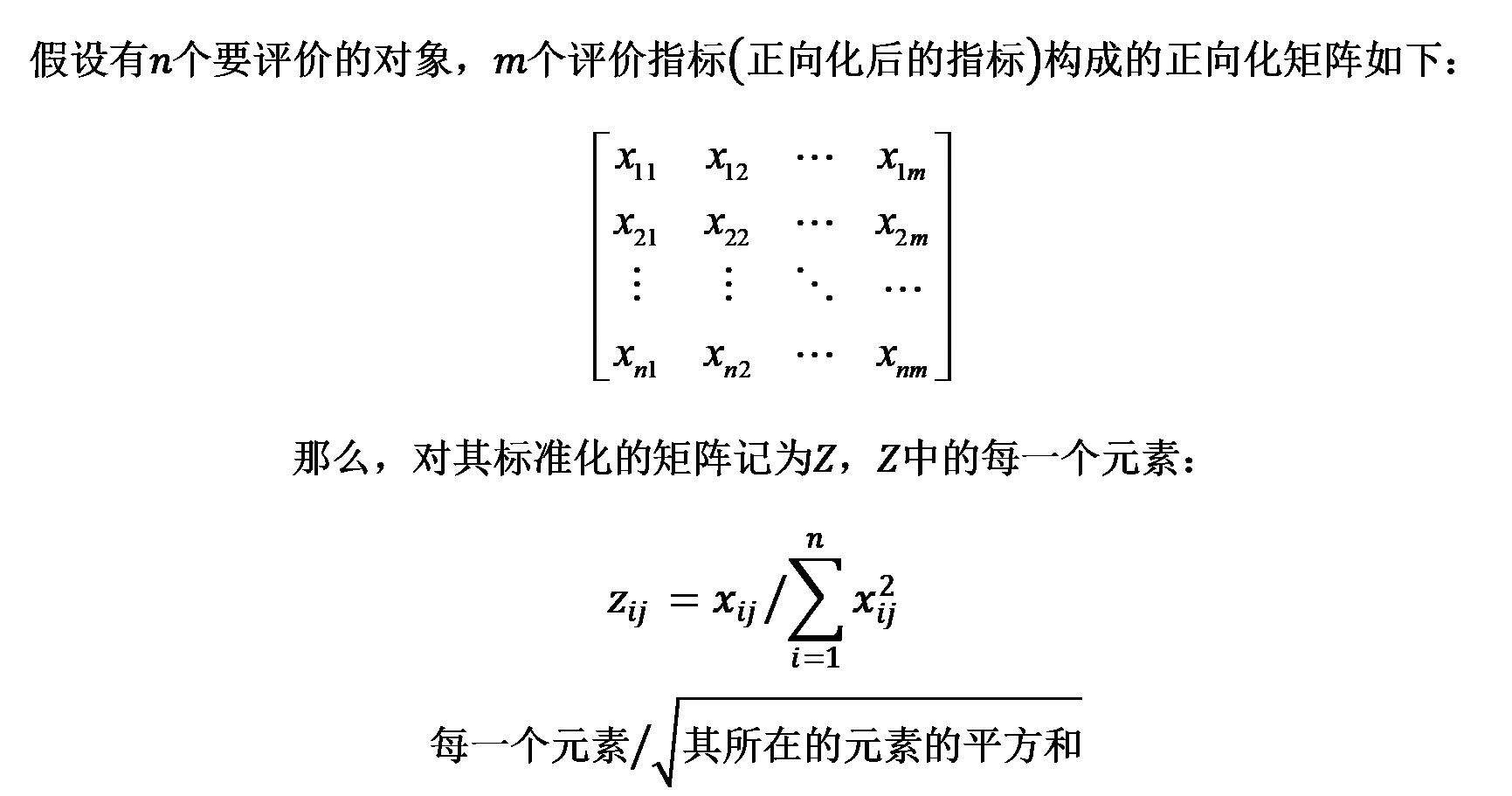TOPSIS算法（优劣解距离法）

TOPSIS法是一种常用的综合评价方法，能充分利用原始数据的信息，所得出结果能精确地反映各评价方案之间的差距。

基本过程

先将原始数据矩阵统一指标类型（一般正向化处理）得倒正向化矩阵，在对正向化的矩阵进行标准化处理以消除个别指标量纲的影响，并找到有限方案中的最优方案和最劣方案，然后分别计算各评价对象与的最优方案和最劣方案间的距离，获得各评价对象与最优方案的相对接近程度，以此作为评价优劣的依据。该方法对数据分布及样本含量没有严格的限制，数据计算简单易行。

常见的四种指标

指标名称 指标特点 例子
极大型（效益型）指标 越大（多）越好 成绩、CDP增速、企业利润
极小型（成本型）指标 越小（少）越好 费用、坏品率、污染程度
中间型指标 越接近某个值越好 水质量评估时的PH值
区间型指标 落在某个区间最好 体温、水中植物性营养物量

第一步：将原始矩阵正向化

所谓将原式矩阵正向化，就是要将所有的指标类型统一转化为极大型指标。（转换的函数形式可以不唯一）

1、极小型 → 极大型

公式
极小型转为极大型公式.png

如果所有元素均为正数，也可以使用1/x

1、中间型指标 → 极大型指标

中间型指标：总体既不要太大也不要太小，取某特定值最好（如水质量评估PH值）


正向化公式.png

2、区间型指标 → 极大型指标

区间型指标：指标值落在某个区间内最好（例如人的体温在36℃~37℃区间比较安全）

7-22-02.png

第二步：正向化矩阵标准化

标准化的目的是消除不同指标量纲的影响

03.png

第三步：计算得分

04.png

模型拓展

带权重的TOPSIS

05.png

TOPSIS算法matlab实现

主函数

第一步：载入数据

数据处理方法

  1. 在工作区右键，点击新建（Ctrl+N)，输入变量名称为X

  2. 在Excel中复制数据，再回到Excel中右键，点击粘贴Excel数据（Ctrl+Shift+V）

  3. 关掉这个窗口，点击X变量，右键另存为，保存为mat文件（下次就不用复制粘贴了，只需使用load命令即可加载数据）

  4. 注意，代码和数据要放在同一个目录下哦，且Matlab的当前文件夹也要是这个目录。

1
2
3
4
```
	clear;clc
	load data_water_quality.mat %加载保存的数据
```

第二步：判断数据是否需要正向化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
```		
	[n,m] = size(X); % 保存矩阵行数和列数
	disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标']) % 统计矩阵行列数并输出 
	Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理，需要请输入1 ，不需要输入0：  ']); %字符串合并，使用空格或“,”连接两串字符
	if Judge == 1
	    Position = input('请输入需要正向化处理的指标所在的列： ');
	    disp('请输入需要处理列的指标类型（1：极小型， 2：中间型， 3：区间型） ') % 确定对应列指标类型
	    Type = input('例如：第2列是极小型，第3列是区间型，第6列是中间型，就输入[1,3,2]：  ');
	    % Position和Type是两个同维度的行向量
	    for i = 1 : size(Position,2)  %这里需要对这些列分别处理，因此我们需要知道一共要处理的次数，即循环的次数
	        X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));
	    % Positivization是我们自己定义的函数，其作用是进行正向化，其一共接收三个参数
	    % 第一个参数是要正向化处理的那一列向量 X(:,Position(i))，X(:,n)表示取第n列的全部元素
	    % 第三个参数是告诉函数我们正在处理的是原始矩阵中的哪一列
	    % 该函数有一个返回值，它返回正向化之后的指标，我们可以将其直接赋值给我们原始要处理的那一列向量
	    end
	    disp('正向化后的矩阵 X =  ')
	    disp(X)
	end
```