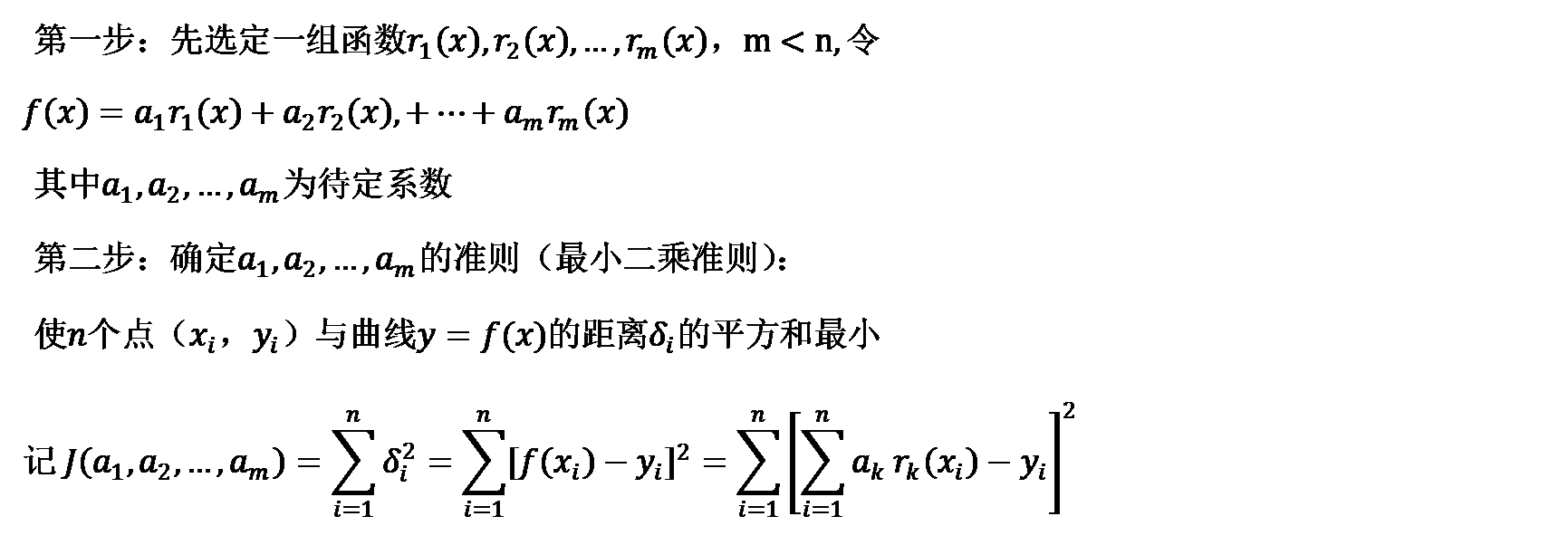插值与拟合

前言

概述

在题中遇到大量数据需要处理时，题目给出的数据往往都存在坏点数据或数据异常。而数据拟合、参数估计、插值等数据处理算法往往是处理这些数据的关键。

基本概念

在实际中，常常要处理由实验或测量所得到的一些离散数据。插值与你和方法就是要通过这些数据去确定某一类已知函数的参数或寻求某个近似函数，使所得到的近似函数与已知数据有较高的拟合精度。

如果要求这个近似函数（曲线或曲面）经过所已知的所有数据点，则称此类问题为插值问题。（不需要函数表达式）

如果不要近似函数通过所有数据点，而是要求它能够较好地反映数据变化规律的近似函数的方法称为数据拟合。（必须有函数表达式）
近似函数不一定（曲线或曲面）通过所有的数据点

插值与拟合的区别和联系

1、联系

都是根据实际中一组已知的数据来构造一个能够反映数据变化规律的近似函数的方法

2、区别

插值问题不一定得到近似函数的表达式，仅通过插值方法找到位置点对应的值。数据拟合要求得倒一个具体的近似函数的表达式。

插值

插值的使用及求解

当数据量不够，需要补充，且认定已有数据可信时，通常利用函数插值方法。

插值方法

1.最近邻算法插值（一维插值）
2.拉格朗日插值算法（一维插值）
3.双线性内插算法（二维插值）
4.分段线性插值（二维插值）
5.三次样条插值（二维插值）
6.克里金插值（地理学）
7.反距离权重插值算法（地理学）

插值的MATLAB实现

实现分段线性插值不需要编写函数程序，matlab提供了内部的功能函数

interp1(一维插值)
interp2(二维插值)
interp3(三维插值)
intern(n维插值)

一维插值

1
2
3
4
5
6
7
8
```
	yi = interp1(x,y,xi,'method') % x,y为插值节点；xi是被插值点；method是插值方法；yi是xi出的插值点的函数值
	% 'nearest'：最佳邻近插值
	% 'linear'：线性插值
	% 'spline'：三次样条插值
	% 'cubic'：立方插值
	% 缺省时：分段线性插值
```

注：所有的插值方法都要求x是单调的，并别xi不能够超过x的范围。

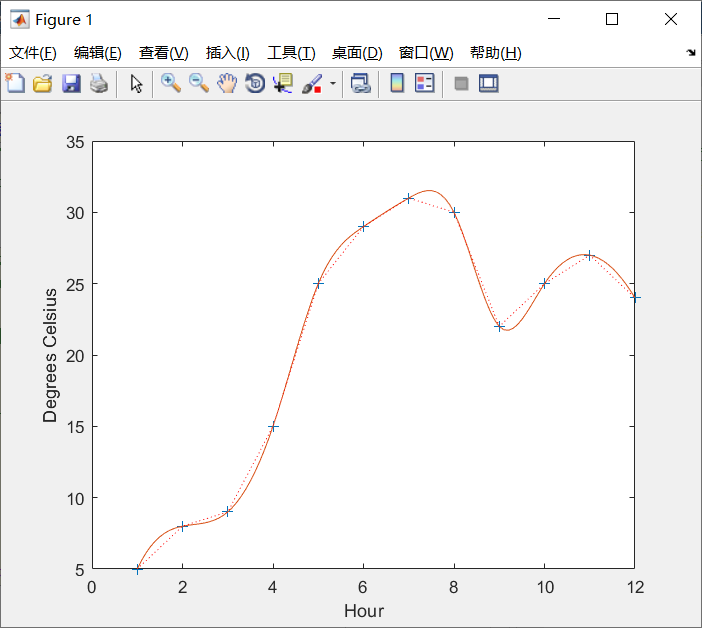
例：从1点到12点的11小时内，每隔1小时测量一次温度，测得的温度的数值依次为：5，8，9，15，25，39，31，30，22，25，17，24，试估计每隔1/10小时的温度值。

1
2
3
4
5
6
7
8
```
	hours = 1:12;
	temps = [5 8 9 15 25 29 31 30 22 25 27 24];
	h = 1:0.1:12; % 插值区间
	t = interp1(hours,temps,h,'spline'); % 使用三次样条插值方法，得到插值后的矩阵t
	plot(hours,temps,'+',h,t,hours,temps,'r:'); % 将插值前与插值后的函数图像画出
	xlabel('Hour'),ylabel('Degrees Celsius') % 横纵坐标名
```

输出
7_24_01.png

二维插值函数

1
2
3
4
5
6
```
	z = interp2(x0,y0,z0,x,y,'method') % x0,y0为插值节点；x,y是被插值点；method是插值方法；z是被插值点的函数值
	% 'nearest'：最佳邻近插值
	% 'linear'：线性插值
	% 'cubic'：立方插值
```

注：要求x0，y0电调；x，y可取为矩阵，或x取行向量，y取为列向量x，y的值分别不能超出x0，y0的范围

例：测得平板表面3×5网格点出的温度分别为：

82 81 80 82 84
79 63 61 65 81
84 84 82 85 86
试作出平板标目暗的温度分布曲线z=f(x,y)的图形

1.先在三位坐标画出原始数据，画出粗糙的温度分布曲线图

1
2
3
4
5
6
```
	x = 1:5;
	y = 1:3;
	temps = [82 81 80 82 84 ;79 63 61 65 81;84 84 82 85 86];
	mesh(x,y,temps) %未插值前三维图像
```

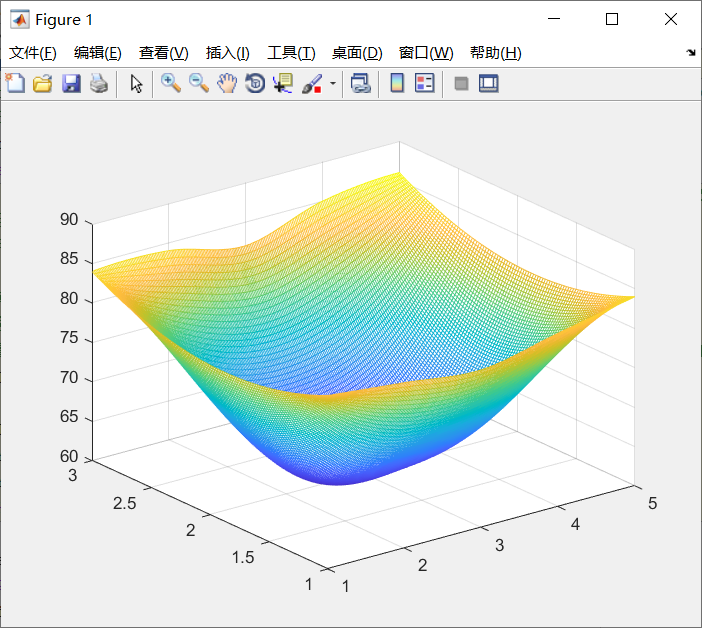
2.以平滑数据在x,y方向是每隔0.02个单位进行插值

1
2
3
4
5
6
```
	xi = 1:0.02:5;
	yi = 1:0.02:3;
	zi = interp2(x,y,temps,xi',yi,'cubic') %空间二维插值
	mesh(xi,yi,zi)
```

输出：
7_24_02.png

拟合

拟合的使用及求解

对于情况复杂的实际问题（因素不易化简，作用机理不详）可直接使用数据组建模，寻找简单的因果变量之间的数量关系，从而对未知的情形作预报。这样组建的模型为拟合模型。
拟合模型的组件主要是处理好观测数据的误差，使用数学表达式从数量上近似因果变量之间爱你的关系。拟合模型的组件是通过对有关变量的观测数据的观察、分析和选择恰当的数学表达式得到的。

直线拟合和曲线拟合

直线拟合

曲线拟合

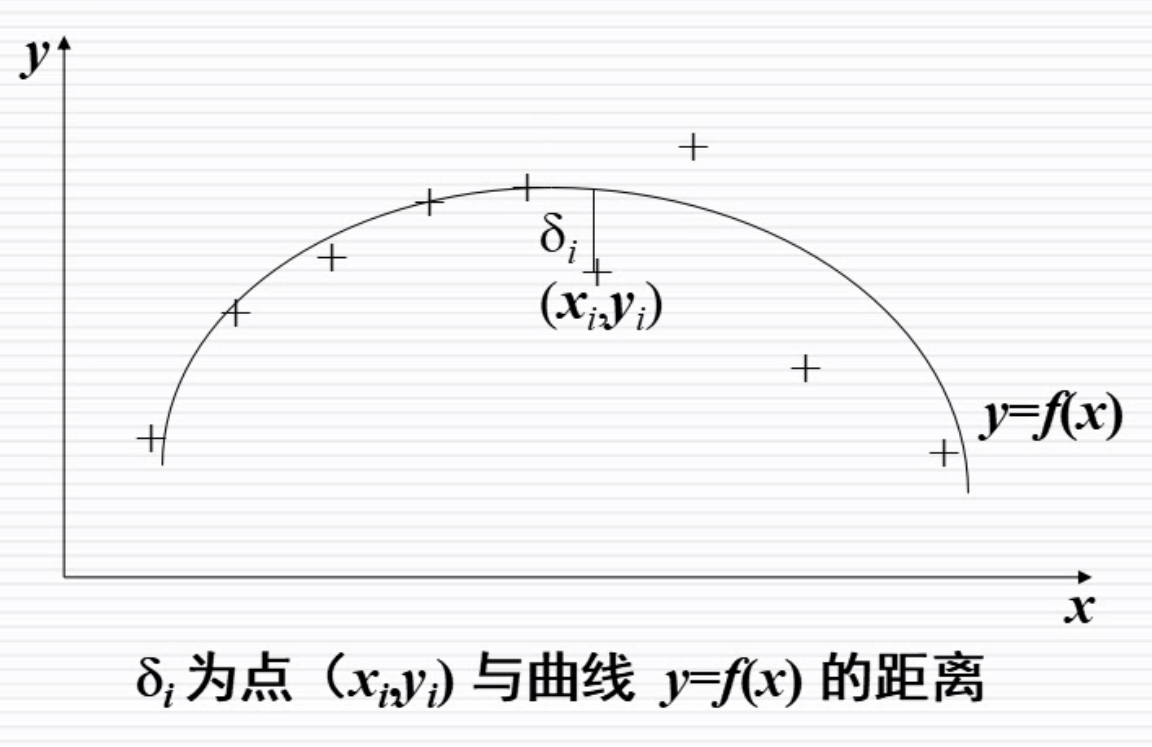
问题提出：

已知一组（二维）数据，即平台上n个点(xi,yi)i=1,…,n，寻求一个函数（曲线）y=f(x)，使f(x)在某种准则下与所有数据点最为接近，即曲线拟合得最好

7_24_03.PNG

曲线拟合最常用解法——线性最小二乘法基本思路

7_24_04.PNG

用MATLAB作线性最小二乘拟合

1
2
3
```
	a = polyfit(x,y,m) %输入相同长度的数组x,y; m为拟合多项式次数
```

多项式在x处的值y可以用以下命令计算：

1
2
3
```
	y = polyval(a,x)
```

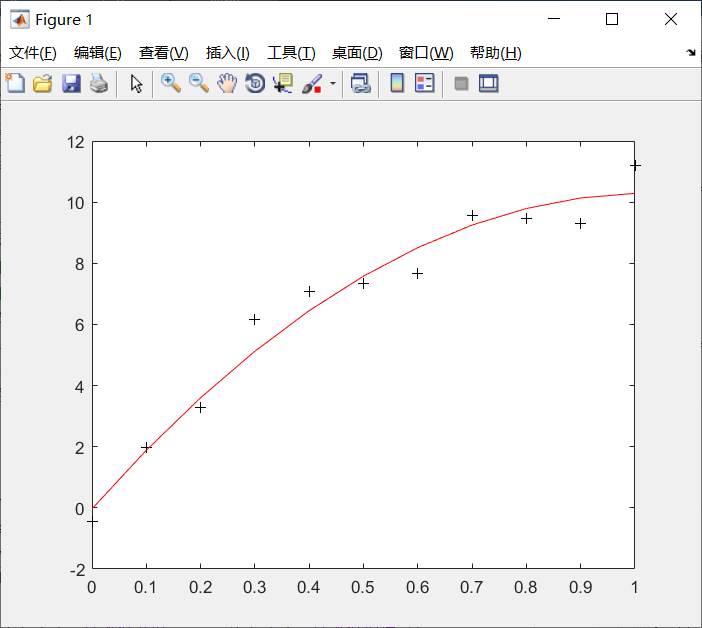
实例代码：

1
2
3
4
5
6
7
```
	x = 0:0.1:1;
	y = [-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];
	A = polyfit(x,y,2)
	z = polyval(A,x)
	plot(x,y,'k+',x,z,'r')
```

输出：

A =
-9.8108 20.1293 -0.0317

7_24_05.png